Strength of Materials Formulas

Stress

where,       σ=normal stress, or tensile stress, p_a

                  P=force applied, N 

                  A=cross-sectional area of the bar, m²

                    =shearing stress, P_a

                  As=total area in shear, m²

Strain

where,

                =tensile or compressive strain, m/m

                =total elongation in a bar, m

                =original length of the bar, m

Hooke's Law

Stress is proportional to strain

where,

E=proportionality constant called the elastic modulus or modulus of elasticity or Young’s modulus, P_a

Piosson's Ratio

where,

                v=Poisson’s ratio

                =lateral strain

                =axial strain

Unit Volume Change

where,

                  =change in volume

                  =original volume

                  =strain

                  =Poisson’s ratio

Elongation due to its weight

where,

=total elongation in a material which hangs vertically under its own weight              

W=weight of the material

Thin Rings

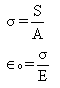
where,

                =Circumferential or hoop Stress

                S=Circumferential or hoop tension

                A=Cross-sectional area

                =Circumferential strain

                E=Young’s modulus

Strain Energy

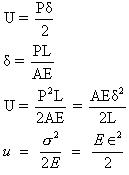
where,

                U=total energy stored in the bar or strain energy

                P=tensile load

   =total elongation in the bar

    L=original length of the bar

    A=cross-sectional area of the bar

    E=Young’s modulus

                U=strain energy per unit volume  

                 

Thin Walled Pressure vessels

where,

                =normal or circumferential or hoop stress in cylindrical vessel, P_a

                =normal or circumferential or hoop stress in spherical vessel,  P_a  and longitudinal stress around the circumference

                  P=internal pressure of cylinder, P_a

                  r=internal radius, m

                  t=thickness of wall, m

Mohr's Circle for Biaxial Stress

Pure Shear

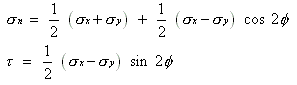
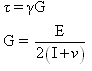
where,

                =Shearing Stress, P_a

                =Shearing Strain or angular deformation

                G=Shear modulus, P_a

                E=Young’s modulus, P_a

                V=Poisson’s ratio

Torsion formula for Thin walled tubes

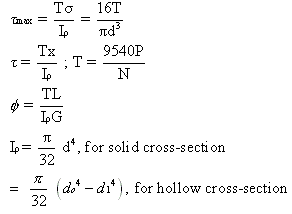
where,

               =maximum shearing stress, P_a

               =Shearing stress at any point a distance x from the centre of a section

                r=radius of the section, m

                d=diameter of a solid circular shaft, m

               =polar moment of inertia of a cross-sectional area, m⁴

                T=resisting torque, N-m

                N= rpm of shaft

                P=power, kW

               =angle of twist, radian

                L=length of shaft, m

                G=shear modulus, P_a

                d_o=outer diameter of hollow shaft, m

                di=inner diameter of hollow shaft, m

and

               

Torsion formula for Circular Shafts

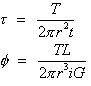
where,

                =I_p, polar moment of inertia for thin-walled tubes

                r=mean radius

                t=wall thickness

Flexure Formula

where,    

                =Stress on any point of cross-section at distance y from the neutral axis

               =stress at outer fibre of the beam

               c=distance measured from the neutral axis to the most remote fibre of the beam

                I=moment of inertia of the cross-sectional area about the centroidal axis

Shear Stress In Bending

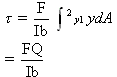
where,    

                F=Shear force

                Q=statistical moment about the neutral axis of the cross-section

                b=width

                I=moment of inertia of the cross-sectional area about the Centroidal axis.

Thin-Walled Hollow Members (Tubes)

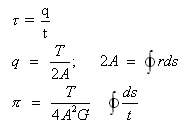
where,      =shearing stress at any point of a blue

                  t=thickness of tube

                  q=shear flow

                  T=applied torque

                  R=distance between a reference point and segment ds

                  Π=angle of twist of a hollow tube

Stress Concentration

Curved Beam in Pure Bending

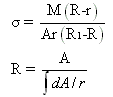
where,     =normal stress

                 M=bending moment

                 dA=cross-sectional area of an element

                 r=distance of curved surface from the centre of curvature

                 A=cross-sectional area of beam

                 R=distance of neutral axis from the centre of curvature

                 R₁=distance of centroidal axis from the centre of curvature

Bending of a Beam

(a) Bending of a Beam Supported at Both Ends

(b) Bending of a Beam Fixed at one end

where,     d= bending displacement, m

                F=force applied, N

                I=length of the beam, m

                a=width of beam, m

                b=thickness of beam, m

                Y=Young’s modulus, N/m²