Beam Deflections: Moment-Area Method

Area-moment method involves the area of the moment diagram.

Theorem 1

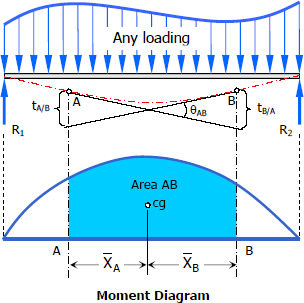
The change in slope between the tangents drawn to the elastic curve at any two points A and Bis equal to the product of 1/EI multiplied by the area of the moment diagram between these two points, provided that the elastic curve is continuous between the two points. In symbol,

Theorem 2

The deviation of any point B relative to the tangent drawn to the elastic curve at any other point A, in a direction perpendicular to the original position of the beam, is equal to the product of 1/EI multiplied by the moment of an area about B of that part of the moment diagram between points A and B, provided that the elastic curve is continuous between the two points. In symbol,

and

Rules of Sign

 •The deviation at any point is positive if the point lies above the tangent, negative if the point is below the tangent.

•Measured from left tangent, if θ is counterclockwise, the change of slope is positive, negative if θ is clockwise.