Strength of Materials

Strength of Materials most often refers to various methods of calculating stresses in structural members, such as beams, columns and shafts. The methods that can be employed to predict the response of a structure under loading and its susceptibility to various failure modes may take into account various properties of the materials other than material (yield or ultimate) strength. For example failure in buckling is dependent on material stiffness (Young's Modulus).


The strength of a material is its ability to withstand an applied stress without failure. The applied stress may be tensile,compressive, or shear. Strength of materials is a subject which deals with loads, deformations and the forces acting on the material. A load applied to a mechanical member will induce internal forces within the member called stresses. Those stresses acting on the material cause deformations of the material. Deformation of the material is called strain, while the intensity of the internal forces are called stress. The strength of any material relies on three different type of analytical method: strength, stiffness and stability, where strength refers to the load carrying capacity, stiffness refers to the deformation or elongation, and stability means refers to the ability to maintain its initial configuration. Material yield strength refers to the point on the engineering stress-strain curve (as opposed to true stress-strain curve) beyond which the material experiences deformations that will not be completely reversed upon removal of the loading. The ultimate strength refers to the point on the engineering stress-strain curve corresponding to the stress that produces fracture.

Types of Loadings

Transverse loading - Forces applied perpendicular to the longitudinal axis of a member. Transverse loading causes the member to bend and deflect from its original position, with internal tensile and compressive strains accompanying change in curvature. It also induces shear forces that cause shear deformation of the material and increase the transverse deflection of the member.
Axial loading - The applied forces are collinear with the longitudinal axes of the member. The forces cause the member to either stretch or shorten.
Torsional loading - Twisting action caused by a pair of externally applied equal and oppositely directed couples acting on parallel planes or by a single external couple applied to a member that has one end fixed against rotation.


Loads applied to the beam may consist of a concentrated load (load applied at a point), uniform load, uniformly varying load, or an applied couple or moment. These loads are shown in the following figures.

Stress Terms

Uniaxial stress is expressed by

where F is the force [N] acting on an area A [m²]. The area can be the undeformed area or the deformed area, depending on whether engineering stress or true stress is of interest.

Compressive Stress is the stress state caused by an applied load that acts to reduce the length of the material in the axis of the applied load, in other words the stress state caused by squeezing the material. A simple case of compression is the uniaxial compression induced by the action of opposite, pushing forces. Compressive strength for materials is generally higher than their tensile strength.

Tensile stress is the stress state caused by an applied load that tends to elongate the material in the axis of the applied load, in other words the stress caused by pulling the material. The strength of structures of equal cross sectional area loaded in tension is independent of shape of the cross section. Materials loaded in tension are susceptible to stress concentrations such as material defects or abrupt changes in geometry.

Shear stress is the stress state caused by a pair of opposing forces acting along parallel lines of action through the material, in other words the stress caused by faces of the material sliding relative to one another. 

Strength terms

Yield strength is the lowest stress that produces a permanent deformation in a material. In some materials, like aluminium alloys, the point of yielding is hard to define, thus it is usually given as the stress required to cause 0.2% plastic strain. This is called a 0.2% proof stress.
Compressive strength is a limit state of compressive stress that leads to failure in the manner of ductile failure (infinite theoretical yield) or in the manner of brittle failure.
Tensile strength or ultimate tensile strength is a limit state of tensile stress that leads to tensile failure in the manner of ductile failure (yield as the first stage of failure, some hardening in the second stage and breakage after a possible "neck" formation) or in the manner of brittle failure. Tensile strength can be quoted as either true stress or engineering stress.
Fatigue strength is a measure of the strength of a material or a component under cyclic loading, and is usually more difficult to assess than the static strength measures. Fatigue strength is given as stress amplitude or stress range (Δσ = σ_max − σ_min), usually at zero mean stress, along with the number of cycles to failure.
Impact strength, is the capability of the material to withstand a suddenly applied load and is expressed in terms of energy. Often measured with the Izod impact strength test or Charpy impact test, both of which measure the impact energy required to fracture a sample. Volume, modulus of elasticity, distribution of forces, and yield strength effect the impact strength of a material. In order for a material or object to have a higher impact strength the stresses must be distributed evenly throughout the object. It also must have a large volume with a low modulus of elasticity and a high material yield strength.

Strain terms

Deformation of the material is the change in geometry when stress is applied (in the form of force loading, gravitational field, acceleration, thermal expansion, etc.). Deformation is expressed by the displacement field of the material.
Strain or reduced deformation is a mathematical term to express the trend of the deformation change among the material field. Strain is the deformation per unit length. For uniaxial loading - displacements of a specimen (for example a bar element) it is expressed as the quotient of the displacement and the length of the specimen.
Deflection is a term to describe the magnitude to which a structural element bends under a load.

Stress-strain relations

Elasticity is the ability of a material to return to its previous shape after stress is released. In many materials, the relation between applied stress and the resulting strain is directly proportional (up to a certain limit), and a graph representing those two quantities is a straight line.
Plasticity or plastic deformation is the opposite of elastic deformation and is accepted as unrecoverable strain. Plastic deformation is retained even after the relaxation of the applied stress. Most materials in the linear-elastic category are usually capable of plastic deformation. Brittle materials, like ceramics, do not experience any plastic deformation and will fracture under relatively low stress. Materials such as metals usually experience a small amount of plastic deformation before failure while ductile metals such as copper and lead or polymers will plasticly deform much more.

Strength of Materials Formulas

Stress

where,       σ=normal stress, or tensile stress, p_a

                  P=force applied, N 

                  A=cross-sectional area of the bar, m²

                    =shearing stress, P_a

                  As=total area in shear, m²

Strain

where,

                =tensile or compressive strain, m/m

                =total elongation in a bar, m

                =original length of the bar, m

Hooke's Law

Stress is proportional to strain

where,

E=proportionality constant called the elastic modulus or modulus of elasticity or Young’s modulus, P_a

Piosson's Ratio

where,

                v=Poisson’s ratio

                =lateral strain

                =axial strain

Unit Volume Change

where,

                  =change in volume

                  =original volume

                  =strain

                  =Poisson’s ratio

Elongation due to its weight

where,

=total elongation in a material which hangs vertically under its own weight              

W=weight of the material

Thin Rings

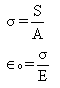
where,

                =Circumferential or hoop Stress

                S=Circumferential or hoop tension

                A=Cross-sectional area

                =Circumferential strain

                E=Young’s modulus

Strain Energy

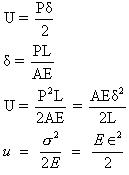
where,

                U=total energy stored in the bar or strain energy

                P=tensile load

   =total elongation in the bar

    L=original length of the bar

    A=cross-sectional area of the bar

    E=Young’s modulus

                U=strain energy per unit volume  

                 

Thin Walled Pressure vessels

where,

                =normal or circumferential or hoop stress in cylindrical vessel, P_a

                =normal or circumferential or hoop stress in spherical vessel,  P_a  and longitudinal stress around the circumference

                  P=internal pressure of cylinder, P_a

                  r=internal radius, m

                  t=thickness of wall, m

Mohr's Circle for Biaxial Stress

Pure Shear

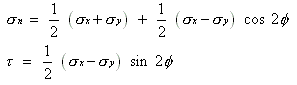
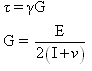
where,

                =Shearing Stress, P_a

                =Shearing Strain or angular deformation

                G=Shear modulus, P_a

                E=Young’s modulus, P_a

                V=Poisson’s ratio

Torsion formula for Thin walled tubes

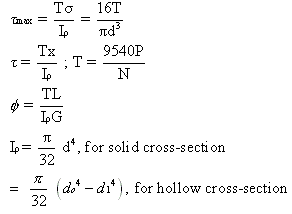
where,

               =maximum shearing stress, P_a

               =Shearing stress at any point a distance x from the centre of a section

                r=radius of the section, m

                d=diameter of a solid circular shaft, m

               =polar moment of inertia of a cross-sectional area, m⁴

                T=resisting torque, N-m

                N= rpm of shaft

                P=power, kW

               =angle of twist, radian

                L=length of shaft, m

                G=shear modulus, P_a

                d_o=outer diameter of hollow shaft, m

                di=inner diameter of hollow shaft, m

and

               

Torsion formula for Circular Shafts

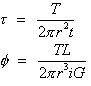
where,

                =I_p, polar moment of inertia for thin-walled tubes

                r=mean radius

                t=wall thickness

Flexure Formula

where,    

                =Stress on any point of cross-section at distance y from the neutral axis

               =stress at outer fibre of the beam

               c=distance measured from the neutral axis to the most remote fibre of the beam

                I=moment of inertia of the cross-sectional area about the centroidal axis

Shear Stress In Bending

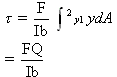
where,    

                F=Shear force

                Q=statistical moment about the neutral axis of the cross-section

                b=width

                I=moment of inertia of the cross-sectional area about the Centroidal axis.

Thin-Walled Hollow Members (Tubes)

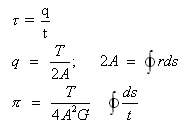
where,      =shearing stress at any point of a blue

                  t=thickness of tube

                  q=shear flow

                  T=applied torque

                  R=distance between a reference point and segment ds

                  Π=angle of twist of a hollow tube

Stress Concentration

Curved Beam in Pure Bending

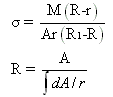
where,     =normal stress

                 M=bending moment

                 dA=cross-sectional area of an element

                 r=distance of curved surface from the centre of curvature

                 A=cross-sectional area of beam

                 R=distance of neutral axis from the centre of curvature

                 R₁=distance of centroidal axis from the centre of curvature

Bending of a Beam

(a) Bending of a Beam Supported at Both Ends

(b) Bending of a Beam Fixed at one end

where,     d= bending displacement, m

                F=force applied, N

                I=length of the beam, m

                a=width of beam, m

                b=thickness of beam, m

                Y=Young’s modulus, N/m²

Failure theories

Maximum Shear stress Theory- This theory postulates that failure will occur in a machine part if the magnitude of the maximum shear stress (tmax) in the part exceeds the shear strength (typ) of the material determined from uniaxial testing.


Maximum normal stress theory- this theory postulates, that failure will occur in machine part if the maximum normal stress in the part exceeds the ultimate tensile stress of the material as determined from uniaxial testing. This theory deals with brittle materials only. The maximum tensile stress should be less than or equal to ultimate tensile stress divided by factor of safety. The magnitude of the maximum compressive stress should be less than ultimate compressive stress divided by factor of safety.


Maximum strain energy theory-this theory postulates that failure will occur when the strain energy per unit volume due to the applied stresses in a part equals the strain energy per unit volume at the yield point in uniaxial testing.


Maximum distortion energy theory- this theory is also known as shear energy theory or von Mises-Hencky theory. This theory postulates that failure will occur when the distortion energy per unit volume due to the applied stresses in a part equals the distortion energy per unit volume at the yield point in uniaxial testing. The total elastic energy due to strain can be divided into two parts. One part causes change in volume, and the other part causes change in shape. Distortion energy is the amount of energy that is needed to change the shape.

Thermal Stress

The stress caused by internal forces created to resist thermal  deformations.

If temperature deformation is permitted to occur freely, no load or stress will be induced in the structure. In some cases where temperature deformation is not permitted, an internal stress is created. The internal stress created is termed as thermal stress.


General Procedure:
• Imagine the structure relieved of all applied loads and constraints so that temperature deformations can occur freely.
• Now imagine sufficient loads applied to the structures to restore it to the specified conditions of restraints.
• From FBD obtain an equation from static equilibrium and obtain an equation from the geometric relations between the temperature and load deformations.

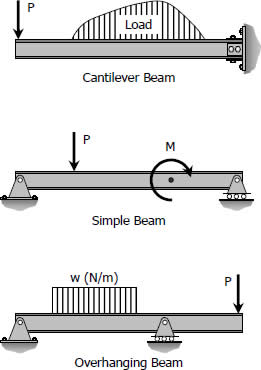
Statically Determinate Structures

Statically determinate beams are those beams in which the reactions of the supports may be determined by the use of the equations of static equilibrium. The beams shown below are examples of statically determinate beams.

Statically Indeterminate Structures

A structure is statically indeterminate when the static equilibrium equations are insufficient for determining the internal forces and reactions on that structure.

• :: the vectorial sum of the forces acting on the body equals zero. This translates to

Σ H = 0: the sum of the horizontal components of the forces equals zero;

Σ V = 0: the sum of the vertical components of forces equals zero;

• : the sum of the moments (about an arbitrary point) of all forces equals zero.

Procedures:

• Obtain equation from static equilibrium

• Compatibility: Obtain equation from deformation

• Apply Hooke's Law

• Solve the unknown

In the beam construction, the four unknown reactions are V_A,V_B, V_C and H_A. The equilibrium equations are:

Σ V = 0:

V_A − F_v + V_B + V_C = 0

Σ H = 0:

H_A − F_h = 0

Σ M_A = 0:

F_v · a − V_B · (a + b) - V_C · (a + b + c) = 0.

The degree of indeterminacy is taken as the difference between the umber of reactions to the number of equations in static equilibrium that can be applied. In the case of the propped beam shown, there are three reactions R₁, R₂, and M and only two equations (ΣM = 0 and ΣF_v = 0) can be applied, thus the beam is indeterminate to the first degree (3 - 2 = 1).

Shear and Moment Diagram

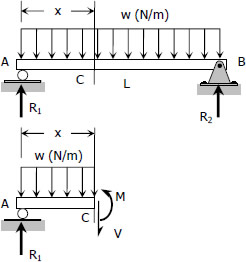
Consider a simple beam shown of length L that carries a uniform load of w (N/m) throughout its length and is held in equilibrium by reactions R₁ and R₂. Assume that the beam is cut at point C a distance of x from he left support and the portion of the beam to the right of C be removed. The portion removed must then be replaced by vertical shearing force V together with a couple M to hold the left portion of the bar in equilibrium under the action of R₁ and wx.

The couple M is called the resisting moment or moment and the force V is called the resisting shear or shear. The sign of V and M are taken to be positive if they have the senses indicated above.

NOTE:

Write shear and moment equations for the beams in the following problems. In each problem, let x be the distance measured from left end of the beam. Also, draw shear and moment diagrams, specifying values at all change of loading positions and at points of zero shear. Neglect the mass of the beam in each problem.

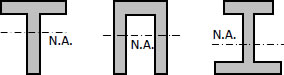
Unsymmetrical Beams

Flexural Stress varies directly linearly with distance from the neutral axis. Thus for a symmetrical section such as wide flange, the compressive and tensile stresses will be the same. This will be desirable if the material is both equally strong in tension and compression. However, there are materials, such as cast iron, which are strong in compression than in tension. It is therefore desirable to use a beam with unsymmetrical cross section giving more area in the compression part making the stronger fiber located at a greater distance from the neutral axis than the weaker fiber. Some of these sections are shown below.

The proportioning of these sections is such that the ratio of the distance of the neutral axis from the outermost fibers in tension and in compression is the same as the ratio of the allowable stresses in tension and in compression. Thus, the allowable stresses are reached simultaneously

Beam Deflections

• Beams are designed for its rigidity rather than its strength when load is applied, the beams deflection must be kept within the tolerable limit.


• Floor beam carrying plastered ceiling beneath them is restricted to maximum deflection of 1/360 L.

Beam Defections: Double Integration Method

The double integration method is a powerful tool in solving deflection and slope of a beam at any point because we will be able to get the equation of the elastic curve.


For a beam with flexural rigidity EI constant, the differential equation is given by

Where y represents the vertical deflection; M is the bending moment at a distance x from the conveniently selected origin; E is the modulus of elasticity or Young's modulus; I is the moment of inertia of the beam section; and the product EI is called the flexural rigidity.

Integrating the above equation once will give us dy/dx which is the equation of the slope of elastic curve, usually denoted by ?. Integrating once more (thus, double integration) will result to y which is the equation of the deflection. We can write it into symbols as follows

and

The constants of integration C₁ and C₂ can be found by applying appropriate boundary conditions.

The first integration y' yields the slope of the elastic curve and the second integration y gives the deflection of the beam at any distance x. The resulting solution must contain two constants of integration since EI y" = M is of second order. These two constants must be evaluated from known conditions concerning the slope deflection at certain points of the beam. For instance, in the case of a simply supported beam with rigid supports, at x = 0 and x = L, the deflection y = 0, and in locating the point of maximum deflection, we simply set the slope of the elastic curve y' to zero.

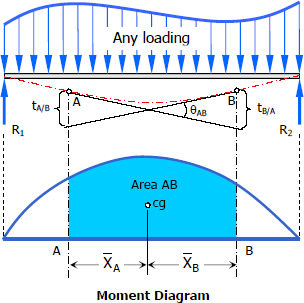
Beam Deflections: Moment-Area Method

Area-moment method involves the area of the moment diagram.

Theorem 1

The change in slope between the tangents drawn to the elastic curve at any two points A and Bis equal to the product of 1/EI multiplied by the area of the moment diagram between these two points, provided that the elastic curve is continuous between the two points. In symbol,

Theorem 2

The deviation of any point B relative to the tangent drawn to the elastic curve at any other point A, in a direction perpendicular to the original position of the beam, is equal to the product of 1/EI multiplied by the moment of an area about B of that part of the moment diagram between points A and B, provided that the elastic curve is continuous between the two points. In symbol,

and

Rules of Sign

 •The deviation at any point is positive if the point lies above the tangent, negative if the point is below the tangent.

•Measured from left tangent, if θ is counterclockwise, the change of slope is positive, negative if θ is clockwise.

Deflection in Simply Supported Beams

The deflection δ at some point B of a simply supported beam can be obtained by the following steps:

 

 

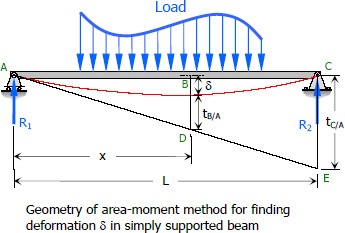
1. Compute 

2. Compute 

3. Solve δ by ratio and proportion (see figure above).